GEMV Tutorial 6: Routes and Fabric DSDs¶

Now that we’ve introduced multiple PEs into our program, instead of duplicating our GEMV problem between them, let’s actually distribute the work for computing a single GEMV.

Learning objectives¶

After completing this tutorial, you should know how to:

Use fabric DSDs fabout_dsd and fabin_dsd to send and receive data between PEs
Utilize asynchronous builtin operations on fabric DSDs
Define a task which is activated by a color

Example overview¶

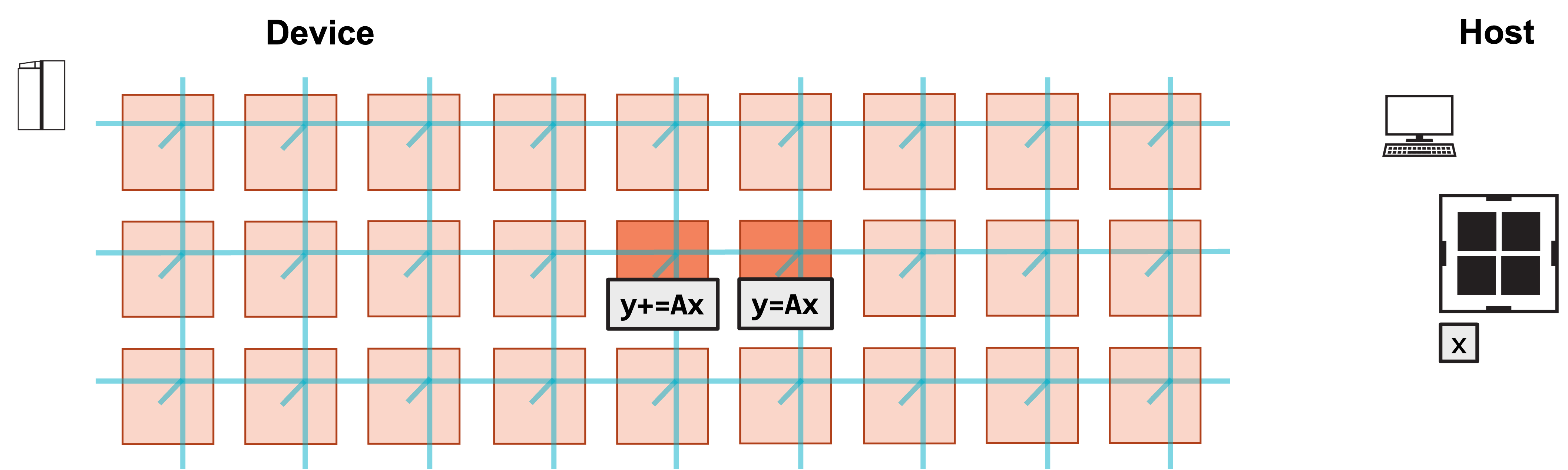
Our program will run on two processing elements (PE).

We will demonstrate the program with a simulated fabric consisting of a 9 x 3 block of PEs.

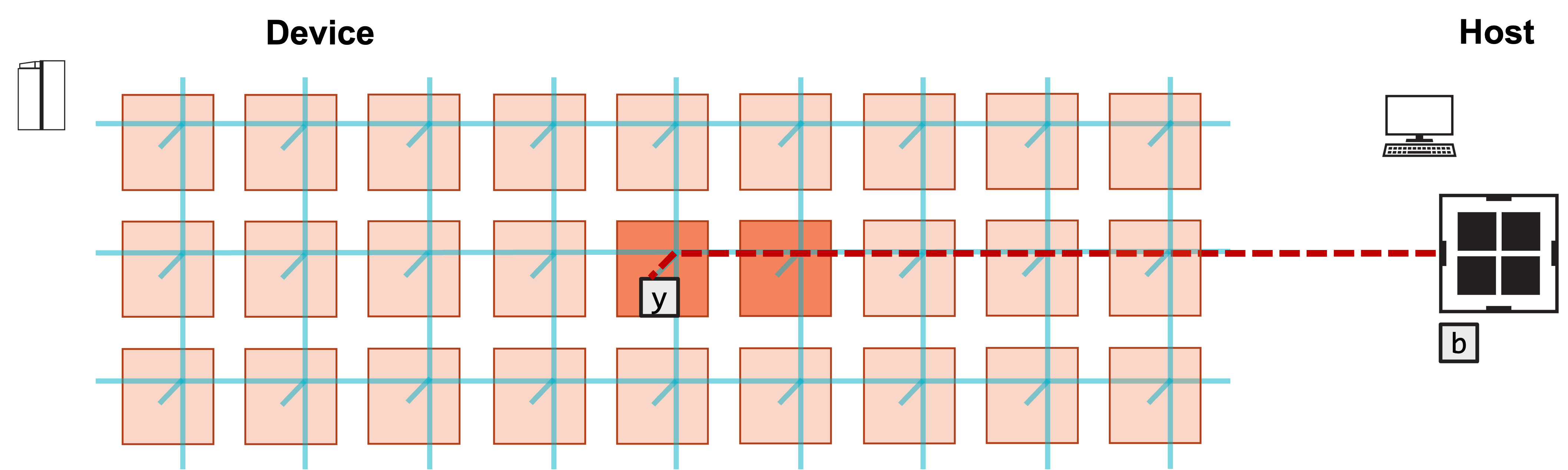
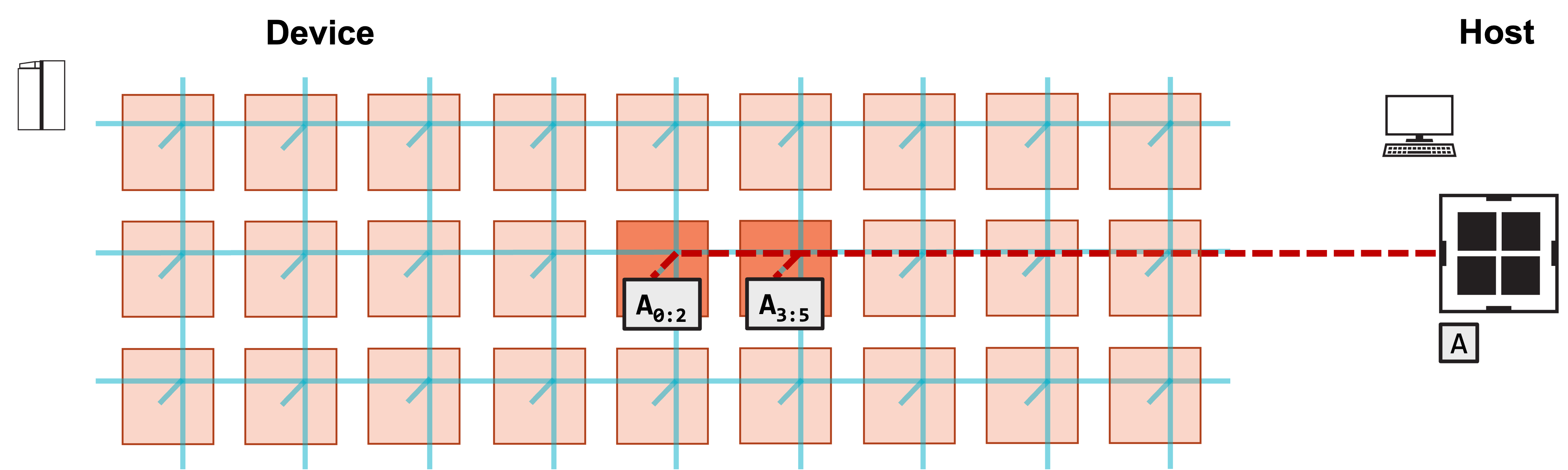
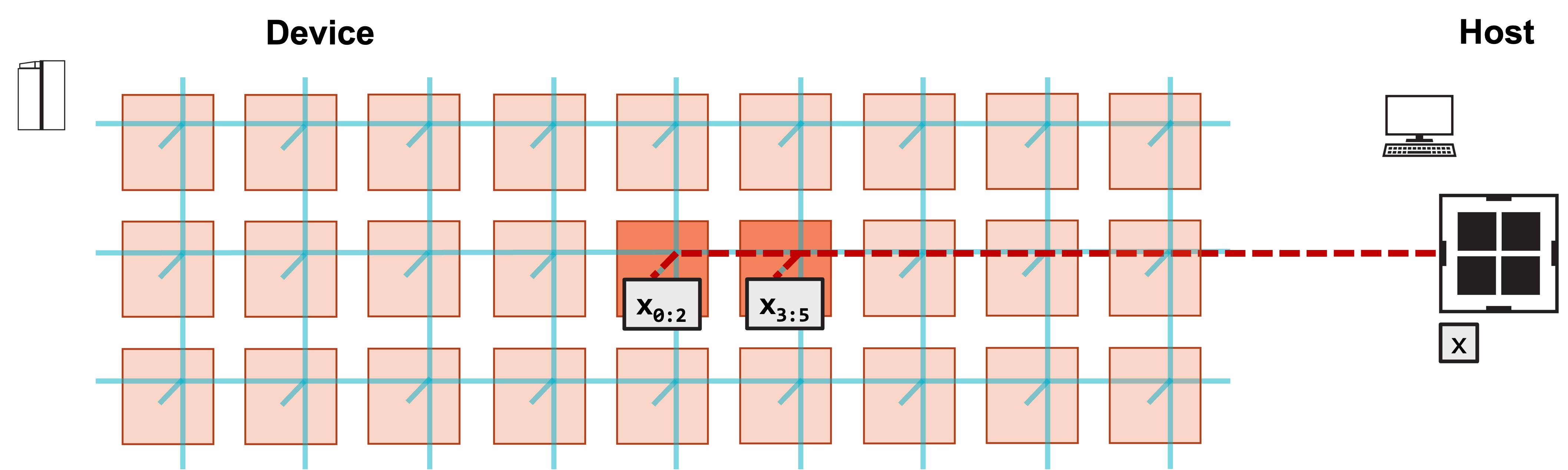
The program will first copy b into the left PE’s y array. Then, it will copy the left half of A’s columns into the left PE, and the right half of A’s columns into the right PE. Similarly, it will copy the the first N/2 elements of x into the left PE, and the last N/2 elements of x into the right PE.

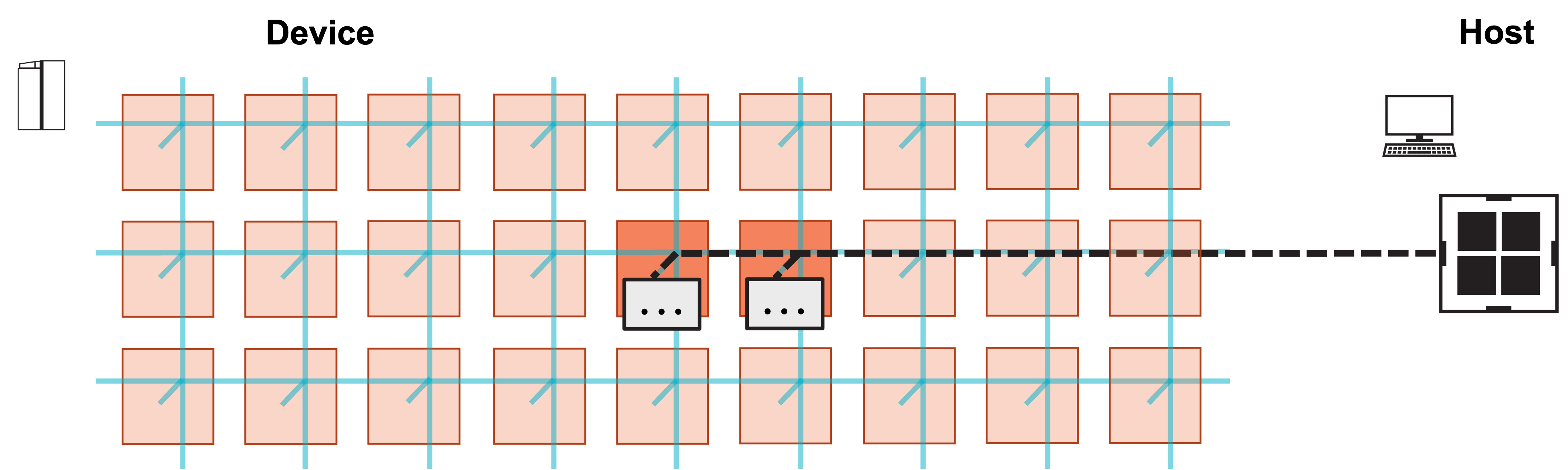
Each PE will then compute A*x for its local pieces of A and x. Thus, both PEs perform a matrix-vector product for an M x N/2 matrix. The PEs will increment their local y arrays by this result.

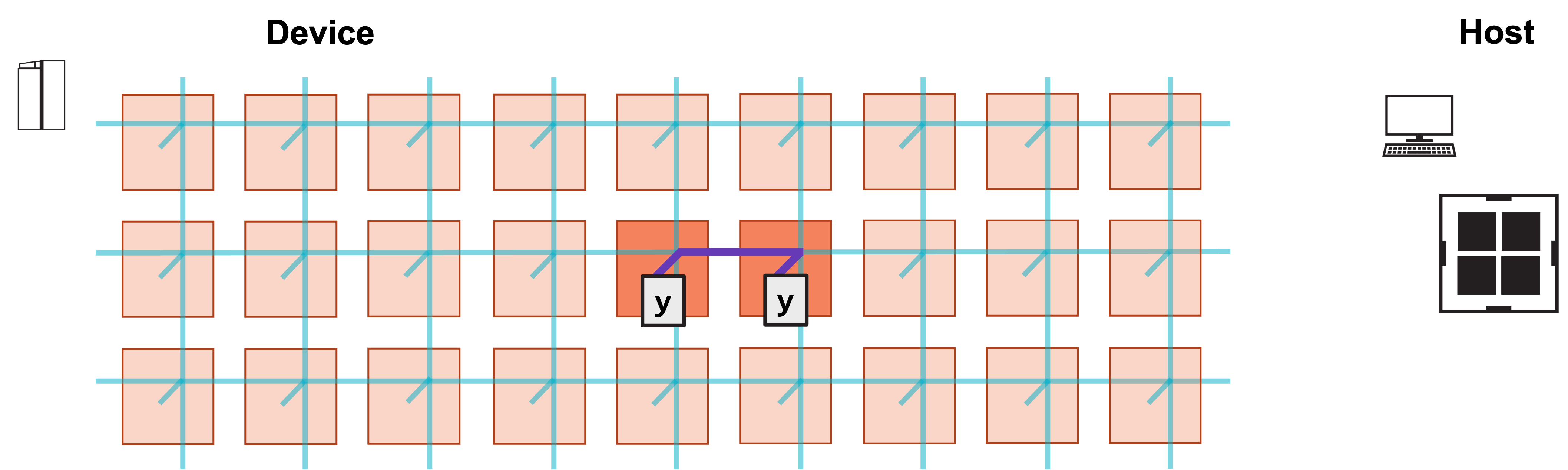
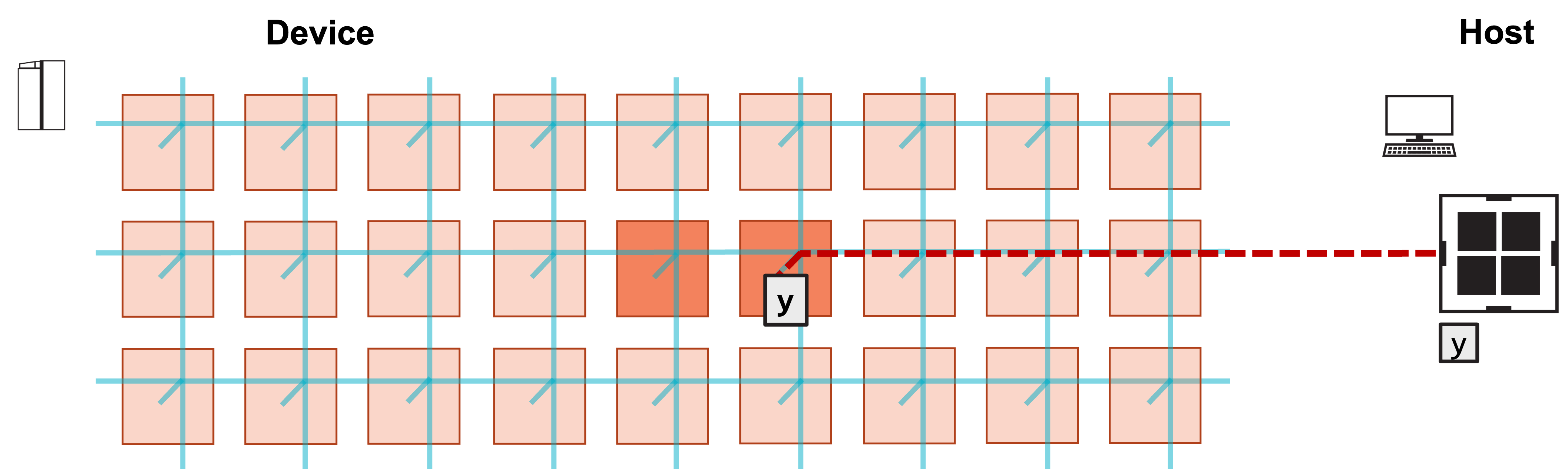
The left PE then sends its y array to the right PE, and the right PE increments its local y array by the received values. Because the left y array contained the contribution from b, the final summed y on the right PE is our GEMV result.

The host then copies y off of the right PE.

Problem Steps¶

Visually, this program consists of the following steps:

1. Host copies b into y array of left PE.

2. Host copies left N/2 columns of A to left PE, right N/2 columns to right PE.

3. Host copies first N/2 elements of x to left PE, last N/2 elements to right PE.

4. Host launches function to compute GEMV.

5. Each PE increments local y by local portion of matrix-vector product Ax.

6. Left PE sends local y to right PE, and right PE increments y by received values.

6. Right PE now contains final result y. Host copies back y from right PE.

Writing the CSL¶

What do we need to modify in our layout to distribute our GEMV between two PEs?

We need to define several new parameters for our two PE programs. This includes a pe_id, used to differentiate between the left and right PEs, and a color, which will be used to route data between the PEs.
We need to set the color configuration on both PEs for the color that will be used to send the left PE’s y array to the right PE.

Let’s take a look at our new layout.csl, included below.

// matrix dimensions on each PE
param M: i16;
param N: i16;

param send_color: color = @get_color(0);

// This example only uses 2 PEs
const memcpy = @import_module("<memcpy_multi/get_params>", .{
  .width = 2,
  .height = 1
});

layout {
  // PE coordinates are (column, row)
  @set_rectangle(2, 1);

  // Left PE (0, 0)
  @set_tile_code(0, 0, "pe_program.csl", .{
    .memcpy_params = memcpy.get_params(0),
    .M = M,
    .N_per_PE = N / 2,
    .pe_id = 0,
    .send_color = send_color
  });

  // Left PE sends its result to the right
  @set_color_config(0, 0, send_color, .{.routes = .{ .rx = .{RAMP}, .tx = .{EAST} }});

  // Right PE (1, 0)
  @set_tile_code(1, 0, "pe_program.csl", .{
    .memcpy_params = memcpy.get_params(1),
    .M = M,
    .N_per_PE = N / 2,
    .pe_id = 1,
    .send_color = send_color
  });

  // Right PE receives result of left PE
  @set_color_config(1, 0, send_color, .{.routes = .{ .rx = .{WEST}, .tx = .{RAMP} }});

  // export symbol names
  @export_name("A", [*]f32, true);
  @export_name("x", [*]f32, true);
  @export_name("y", [*]f32, true);
  @export_name("compute", fn()void);
}

We have two @set_tile_code calls, one for the left PE (0, 0), and one for the right PE (1, 0). Both PEs take a new parameter, N_per_PE, equal to N / 2. This is the number of columns of A that each PE will receive and operate on. Both PEs also receive as a parameter a pe_id: the left PE has pe_id 0, and the right PE has pe_id 1. We’ll see in pe_program.csl how we use pe_id to parameterize the behavior of the program.

We also have two @set_color_config calls, to set the configuration of send_color on each PE:

@set_color_config(0, 0, send_color, .{.routes = .{ .rx = .{RAMP}, .tx = .{EAST} }});
...
@set_color_config(1, 0, send_color, .{.routes = .{ .rx = .{WEST}, .tx = .{RAMP} }});

The router of each PE has five directions: RAMP, NORTH, SOUTH, EAST, WEST. The cardinal directions refer to the routers of neighboring PEs: NORTH is the PE directly above our PE, and so on. RAMP refers to the connection between our PE’s router and its compute element (CE). When setting a route for a color on a given PE, the receive rx and transmit tx fields are from the perspective of the router. Thus, receiving form the RAMP means that our compute element is sending data up to the fabric, where it can then be transmitted across the fabric.

For the left PE (0, 0), send_color will send up the PE’s RAMP to the fabric, and then transmit data to the EAST. For the right PE (1, 0), send_color will receive data from the WEST on the fabric (i.e., from the left PE), and then transmit it down the RAMP to its compute element.

Now let’s take a look at our new pe_program.csl, included below.

param memcpy_params: comptime_struct;

// Matrix dimensions
param M: i16;
param N_per_PE: i16;

// ID of PE (0 is left, 1 is right)
param pe_id: i16;

// Color used to send/recv data between PEs
param send_color: color;

const LAUNCH: color = @get_color(8);
const exit_color: color = @get_color(9);

// memcpy module provides infrastructure for copying data
// and launching functions from the host
const sys_mod = @import_module("<memcpy_multi/memcpy>", @concat_structs(memcpy_params, .{
  .LAUNCH = LAUNCH
}));


// 48 kB of global memory contain A, x, b, y
var A: [M*N_per_PE]f32; // A is stored column major
var x: [N_per_PE]f32;
var y: [M]f32;

// DSDs for accessing A, b, y
// A_dsd accesses column of A
var A_dsd = @get_dsd(mem1d_dsd, .{ .tensor_access = |i|{M} -> A[i] });
var y_dsd = @get_dsd(mem1d_dsd, .{ .tensor_access = |i|{M} -> y[i] });

// ptrs to A, x, b, y will be advertised as symbols to host
var A_ptr: [*]f32 = &A;
var x_ptr: [*]f32 = &x;
var y_ptr: [*]f32 = &y;

// Compute gemv
fn gemv() void {
  // Loop over all columns of A
  for (@range(i16, N_per_PE)) |i| {
    // Calculate contribution to A*x from ith column of A, ith elem of x
    @fmacs(y_dsd, y_dsd, A_dsd, x[i]);
    // Move A_dsd to next column of A
    A_dsd = @increment_dsd_offset(A_dsd, M, f32);
  }
}

fn send_right() void {
  const out_dsd = @get_dsd(fabout_dsd, .{
                    .fabric_color = send_color, .extent = M,
                    .output_queue = @get_output_queue(0)
                  });
  // After fmovs is done, activate exit_task to unblock cmd_stream
  @fmovs(out_dsd, y_dsd, .{ .async = true, .activate = exit_color });
}

fn recv_left() void {
  const in_dsd = @get_dsd(fabin_dsd, .{
                   .fabric_color = send_color, .extent = M,
                   .input_queue = @get_input_queue(1)
                 });
  // After fadds is done, activate exit_task to unblock cmd_stream
  @fadds(y_dsd, y_dsd, in_dsd, .{ .async = true, .activate = exit_color });
}

// Call initialize and gemv functions
fn compute() void {
  gemv();
  if (pe_id == 0) {
    send_right();
  } else {
    recv_left();
  }
}

task exit_task() void {
  sys_mod.unblock_cmd_stream();
}

comptime {
  // When exit_color is activated, exit_task will execute
  @bind_task(exit_task, exit_color);

  // send_color must be blocked so that default task bound to it
  // by compiler does not consume its wavelets before in_dsd
  // receives them in recv_left function
  @block(send_color);

  @export_symbol(A_ptr, "A");
  @export_symbol(x_ptr, "x");
  @export_symbol(y_ptr, "y");
  @export_symbol(compute);
  @rpc(LAUNCH);
}

In addition to our new parameters N_per_PE, pe_id, and send_color, we also introduce a color exit_color. We’ll talk about its use a bit later.

The A array now has size M*N_per_PE instead of M*N, since each PE only stores half the columns. To make our data transfer easier, we also now store A column-major instead of row-major. Notice that A_dsd now accesses M contiguous elements, instead of M elements strided by the row size, since we now store column-major.

Our gemv function operates almost identically to before, except we only loop over N_per_PE columns instead of N columns. Since A is now column-major, @increment_dsd_offset must increment by the length of an entire column instead of by one element. Note that on the left PE, y already contains the elements of b before gemv executes.

Fabric DSDs and async operations¶

The compute function, which is called from the host, first calls gemv to compute the local contribution to y on each PE. Then, the left PE calls send_right, while the right PE calls recv_left.

send_left defines a fabout_dsd, which is used to send wavelets to the fabric along the color send_color. Note that we give this fabout_dsd the extent M, since we intend to send the M elements of y along the fabric. The @fmovs operation copies the M elements accessed by y_dsd into out_dsd. The .async = true field makes this operation asynchronous. The .activate field specifies a color to activate when this operation completes. When this operation completes, exit_color will be activated.

recv_right defines a fabin_dsd to receive the wavelets sent along send_color. The @fadds operation here increments the right PE’s y_dsd by the elements received in in_dsd. Thus, after this operation, y_dsd contains our final GEMV result. This builtin also executes asynchronously, and actives exit_color when complete.

Whenever using fabric DSDs in builtin operations, always make these operations execute asynchronously. Using fabric DSDs synchronously can result in poor performance or deadlocks.

Tasks and activatable colors¶

Now, what does activating exit_color do? In the comptime block, the @bind_task builtin binds exit_color to the task exit_task. When exit_color is activated, exit_task, which unblocks the memcpy command stream, executes. This task must execute on both PEs before control is returned to the host.

Notice that in the comptime block we also call @block(send_color). This builtin sets the initial state of send_color to “blocked”. The compiler inserts a dummy task bound to send_color, but we do not want this task to execute when we receive wavelets along send_color. Instead, on the right PE, we want wavelets sent along send_color to be received by our fabin_dsd.

Writing the host code¶

Our new host code must:

Copy b into the left PE’s y array
Copy the left halves of A and x to the left PE, and the right halves to the right PE
After the device kernel completes, copy y back from the right PE

We explain some features of our new run.py below.

#!/usr/bin/env cs_python

import argparse
import json
import numpy as np

from cerebras.sdk.runtime.sdkruntimepybind import SdkRuntime, MemcpyDataType, MemcpyOrder # pylint: disable=no-name-in-module

# Read arguments
parser = argparse.ArgumentParser()
parser.add_argument('--name', help="the test compile output dir")
parser.add_argument('--cmaddr', help="IP:port for CS system")
args = parser.parse_args()

# Get matrix dimensions from compile metadata
with open(f"{args.name}/out.json", encoding='utf-8') as json_file:
  compile_data = json.load(json_file)

# Matrix dimensions
N = int(compile_data['params']['N'])
M = int(compile_data['params']['M'])

# Construct A, x, b
A = np.arange(M*N, dtype=np.float32).reshape(M,N)
x = np.full(shape=N, fill_value=1.0, dtype=np.float32)
b = np.full(shape=M, fill_value=2.0, dtype=np.float32)

# Calculate expected y
y_expected = A@x + b

# Size of N dimension on each PE
N_per_PE = N // 2

# Construct a runner using SdkRuntime
runner = SdkRuntime(args.name, cmaddr=args.cmaddr)

# Get symbols for A, b, x, y on device
A_symbol = runner.get_id('A')
x_symbol = runner.get_id('x')
y_symbol = runner.get_id('y')

# Load and run the program
runner.load()
runner.run()

# Copy b into y of PE (0, 0)
runner.memcpy_h2d(y_symbol, b, 0, 0, 1, 1, M, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

# Copy A in column major format
# PE (0, 0) gets first N/2 columns; PE (1, 0) gets last N/2 columns
runner.memcpy_h2d(A_symbol, A.transpose().ravel(), 0, 0, 2, 1, M*N_per_PE, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

# PE (0, 0) gets first N/2 elements; PE (1, 0) gets last N/2 elements
runner.memcpy_h2d(x_symbol, x, 0, 0, 2, 1, N_per_PE, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

# Launch the compute function on device
runner.launch('compute', nonblock=False)

# Copy y back from PE (1, 0)
y_result = np.zeros([M], dtype=np.float32)
runner.memcpy_d2h(y_result, y_symbol, 1, 0, 1, 1, M, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

# Stop the program
runner.stop()

# Ensure that the result matches our expectation
np.testing.assert_allclose(y_result, y_expected, atol=0.01, rtol=0)
print("SUCCESS!")

Copying `b` into `y` of left PE¶

We copy b into y of the left PE here:

runner.memcpy_h2d(y_symbol, b, 0, 0, 1, 1, M, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

Notice that the ROI is a single PE, located at (0, 0) in the program rectangle. The right PE (1, 0) is omitted from this memcpy call.

Copying `A` and `x`¶

We copy A and x to the device as follows:

runner.memcpy_h2d(A_symbol, A.transpose().ravel(), 0, 0, 2, 1, M*N_per_PE, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

runner.memcpy_h2d(x_symbol, x, 0, 0, 2, 1, N_per_PE, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

Notice that the ROI is now both PEs, so the memcpy calls copy data into both the left and right PE.

Because we now store A column-major on the PEs, we transpose our A matrix, and then flatten it to a 1D array with ravel(). Each PE gets M*N_per_PE elements, so each PE gets N_per_PE columms of A.

Similarly, each PE gets N_per_PE elements of x.

Copying back result¶

We copy back y from the right PE as follows:

y_result = np.zeros([M], dtype=np.float32)
runner.memcpy_d2h(y_result, y_symbol, 1, 0, 1, 1, M, streaming=False,
  order=MemcpyOrder.ROW_MAJOR, data_type=MemcpyDataType.MEMCPY_32BIT, nonblock=False)

Notice that our ROI now begins at (1, 0), and contains a single PE. Thus, this memcpy call copies back the M elements of y only from the right PE.

Once this call is complete, we then, as in our previous tutorials, check that the received result is correct.

Compiling and running the program¶

Since this program only uses two PEs, we adjust our simulated fabric dimensions accordingly:

$ cslc layout.csl --fabric-dims=9,3 --fabric-offsets=4,1 --params=M:4,N:6 --memcpy --channels=1 -o out
$ cs_python run.py --name out

We use the same command to run. You should see a SUCCESS! message at the end of execution.

Exercises¶

Instead of using two PEs along the same row to compute this GEMV, try using two PEs along the same column.

Next¶

Stay tuned for more tutorials!

SDK Documentation (0.9.0)

GEMV Tutorial 6: Routes and Fabric DSDs

Contents

GEMV Tutorial 6: Routes and Fabric DSDs¶

Learning objectives¶

Example overview¶

Problem Steps¶

Writing the CSL¶

Fabric DSDs and async operations¶

Tasks and activatable colors¶

Writing the host code¶

Copying `b` into `y` of left PE¶

Copying `A` and `x`¶

Copying back result¶

Compiling and running the program¶

Exercises¶

Next¶

SDK Documentation (0.9.0)

GEMV Tutorial 6: Routes and Fabric DSDs

Contents

GEMV Tutorial 6: Routes and Fabric DSDs¶

Learning objectives¶

Example overview¶

Problem Steps¶

Writing the CSL¶

Fabric DSDs and async operations¶

Tasks and activatable colors¶

Writing the host code¶

Copying b into y of left PE¶

Copying A and x¶

Copying back result¶

Compiling and running the program¶

Exercises¶

Next¶

Copying `b` into `y` of left PE¶

Copying `A` and `x`¶